|
www.faxfn.org 3 MODEL We wish here to extend the work of Beacon and Monk (1987) in considering a numerically-solved model with many inputs, none of which are inelastically supplied. We first outline a general model for tackling this sort of problem. We then give a specific example, adopting a Cobb-Douglas technology. The model employs a similar stylised initial data set and the same combined tax and subsidy scheme as used in Beacon and Monk (1987). 3.1 General Model We start with a linear homogeneous production function (3.1) where the output, Q, in the single sector is produced with n labour inputs, L1, L2, ..., Ln and a capital input K. The supply of each labour input Li is a positive function of the real consumption wage, wci, equation (3.2). Capital is a produced factor of production and given that we assume a single sector, the one commodity is used for both capital and consumption purposes. This has the implication that the price of capital and consumption goods cannot diverge. The treatment of capital goods in the work that we have reviewed is either absent (Layard and Jackman, 1980) or ad hoc (Johnson, 1980; Beacon and Monk, 1987). We here wish to consider two possibilities. First we adopt the Keynesian savings function: we assume that savings are a fixed proportion, s, of income. In long run equilibrium, such savings just cover capital depreciation, which occurs at a rate d. This implies that
so that The fact that the capital-output ratio remains constant means that the user cost of capital rp (here taken to be the sum of the interest rate, the rate of depreciation, d and tax) remains constant. A second approach is to take the supply of capital to be infinitely elastic at the existing post-tax rate of return rc. In this formulation, the capital output ratio is dependent on this rate of return and the tax rate, so that This would be the implication if national and international financial markets were perfectly integrated so that there was a unique ruling post-tax rate of return. This assumption is the reverse of that underlying the Keynesian savings function where the domestic supply of finance is taken to determine the level of domestic investment and this supply is price inelastic. Production is taken to be perfectly competitive. This has the implication that the demand for inputs is set such that the value of the marginal product equals the producer price of the factor wpi. Taking the product price as the numeraire, this implies that Equation (3.4) defines the producer price of a factor as a function of the chosen set of factor inputs. Taxes, t, and subsidies, S, drive a wedge between the consumption wage and the producer price of labour, so that Finally, we impose a balanced government budget. We identify only two forms of government expenditure, the labour subsidy and unemployment benefit, and this is paid for by a value-added tax. This government's budget position is expressed as where X(.) is the government's expenditure function, T(.) its tax function, b is the unemployment benefit payment per capita and P is the registered working population. Essentially the model operates in the following way. If the government introduces a subsidy, S, with an appropriate increase in tax to cover the subsidy, this changes the wedge between the real consumption wage and the producer price of labour via equation (3.5). For example, the scheme suggested by Beacon and Monk (1987) introduces a per capita subsidy financed by a proportionate tax. With fixed real consumption wages, this reduces the producer price of labour in the lowest wage groups but, from equation (3.4), increases the producer price of labour for at least one high wage labour group. These input price changes affect producer demand for these inputs and there is a subsequent change in employment and consumption wages in the various labour groups. In general, as a result of these adjustments, total employment changes, with a corresponding alteration in output through equation 3.1. This affects the total bill for unemployment benefit and the total tax take. There therefore has to be an adjustment to the tax rate to rebalance the government budget and this has further impacts on output and employment. To take a simple example, if output and employment have both increased as a result of the first round of the adjustment process, unemployment benefit payments will be lower whilst tax revenues are higher. A reduction in the tax rate in order to reinstate a balanced government budget will here stimulate the supply of all labour inputs as consumption wages rise, further expanding employment and output. Of course other scenarios are possible, including ones in which employment rises but total output falls in the first round of adjustment. 3.2 Specific Formulation 3.2.1 One Labour Input, Keynesian Savings Function The most straightforward case is where the technology is Cobb-Douglas, there is only one labour input and there is a Keynesian savings function. The analysis proceeds by taking total differentials of the relevant equations. Equation 3.7 is derived from the production function. Note here that from equation 3.3a capital inputs are endogenous, rising in equilibrium in line with output, so that only changes in labour inputs are required to predict changes in output. where the dot notation indicates a proportionate change in the relevant variable, aL and aK represent the share of output going to labour and capital respectively (so that aL + aK = 1) and these values are the corresponding coefficients on the input terms in the Cobb-Douglas production function. Equation 3.8 is obtained from taking total differentials of the labour supply functions, where b is the labour supply elasticity. Equation 3.9 is implied by the factor demand equations. Equation 3.10 defines the operation of the wedge. S is the labour subsidy which is assumed to take an initial value of zero, t is the proportionate VAT rate. Equation 3.11 is derived from the total differential of the public sector balanced budget equation This very simple model has two heuristic strengths. First, the results do not depend on any substitution effects: there is no substitution of labour for capital. The point here is not that such substitution effects are unimportant in reality, but rather that employment can be stimulated without substitution and this model identifies such behaviour very clearly. Second, within this type of approach there is the possibility of model instability and again it is pedagogically instructive to consider such instability in the simplest case. If we substitute equation (3.7) into equation (3.9), we get the result that This means that the producer price of labour, and therefore the cost-minimising (profit-maximising) technique, does not vary with the subsidy. Given that output is rising at the same rate as employment in this model, this is not surprising. However, labour supply is a function of the consumption wage. The introduction of a tax and subsidy scheme will change the wedge between the producer and consumption wage, so that labour supply, and therefore output, will in general change with the introduction of a subsidy. Substituting equation (3.12) into equation (3.10) gives and combining this with (3.8) yields Given that the subsidy is only given to labour but taxes are levied on both labour and capital, the consumption wage must rise for a neutral tax/subsidy scheme, even if no unemployment benefit were paid. This implies that in this model employment will always rise under such a scheme, even though no substitution of labour for capital occurs. Moreover, the higher the savings in unemployment benefit that are generated by the increased employment, the more such effects will be magnified. It is instructive to analyse the change in employment a little more formally. Combining equations (3.7), (3.11) and (3.14), simplifying and using the relationship implied by the Cobb-Douglas production function gives We know that the introduction of a subsidy will generate an increase in employment. In equation (3.16) the numerator here is positive. However, the denominator is negative if But this is the necessary and sufficient condition for the government's budget deficit to move into surplus with a fall in the tax rate. This would correspond to an economy operating on the downward section of the Laffer curve. Under these conditions the imposition of a balanced public sector budget renders the economy dynamically unstable with respect to changes in the tax regime. The introduction of a subsidy would lead to a fall in the (unstable) equilibrium employment level. However, the original employment level would be higher than this and, given that the equilibrium is unstable and that a balanced budget is imposed throughout, employment would rise, and taxes fall, continuously. 3.2.2 One Labour Input and a Perfectly Elastic Supply of Capital This model is identical to that outlined in the previous section, except for the fact that in this case the supply of capital is not a constant proportion of national output, but rather is infinitely elastic at the ruling post-tax rate of return. We therefore need to consider changes in the producer price of both inputs of capital and labour as the owners maintain their post-tax return to capital rc.2 This is defined as where rp is the producer price of capital and t is the VAT rate. Where there is a perfectly elastic supply of capital, rc does not vary, so that Totally differentiating equation (3.18) and substituting in (3.19) produces This implies that the introduction of a tax on capital is passed on to the producer. Given the producer price of capital, the demand for capital is derived as Totally differentiating equation (3.21) and substituting in equation (3.20) generates Note that in contrast to the analysis in the previous section with the Keynesian savings function, here capital increases less rapidly than output after an increase in the tax. Changes in output are determined by equation (3.1) and (3.22) We are now able to find the change in the producer price of labour and the consumption wage, which are respectively. We can see here a key aspect of this formulation of the model. With the introduction of the tax/subsidy package, the producer price of labour falls. This is what is powering the substitution of labour for capital. However, for employment to rise, the consumption wage must rise. Compare equation (3.25) with equation (3.13), the equation that identifies the change in the consumption wage where we adopt the Keynesian savings function. It is clear that the negative impact of tax changes on the consumption wage is higher with the perfectly elastic supply of capital. Using equation (3.25), the change in labour supply is and from the government budget constraint and using equation (3.25), the change in the tax rate, dt, is Combining equations (3.26) and (3.27) and rearranging gives the expression for the change in employment, which is Clearly expression (3.28) is more complex than where we assume a Keynesian savings function. In this case, there is no automatic increase in employment. The numerator is negative (as long as aL > t) but the denominator is only negative where 3.2.3 Many labour inputs In the previous subsection we have presented two forms of the model where there are only two factors of production, homogeneous capital and labour, and we have solved the model analytically. Here we present the more general Cobb-Douglas case where there are a number of different labour inputs. Again we present two alternative capital supply functions: the Keynesian savings function and the infinitely elastic capital supply. Both models are solved numerically. The equations for labour supply, the producer price of labour, the consumption wage and the budget constraint are identical for both models. Their form is similar to those for the two-factor models. The i and j subscripts indicate the particular labour sub-group. Therefore labour supply is Producer price of labour is The consumption wage is And the total differential of the public sector balanced budget equation is Where the two models differ is in the determination of output. When we impose the Keynesian savings assumption where For the perfectly elastic supply of capital If equations (3.30) to (3.34) are employed the two alternative models can be expressed in the following equations (3.35) and (3.36). For the model with the Keynesian savings function For the perfectly elastic capital supply the corresponding equations are Equations 3.35 and 3.36 give n+1 equations in n+1 unknowns: the n proportionate employment changes and the change in the tax rate. 3.3 Simulation We have used equations 3.35 and 3.36 as the basis for a set of simulation exercises. These give estimates of the impact of a similar type of tax and subsidy scheme as that investigated in Beacon and Monk (1987): a fixed per capita labour subsidy equal to 5% of the average wage financed through increased general taxation of a VAT type. We start with a stylised representation of the initial equilibrium position of the economy which follows that given in Beacon and Monk (1987). This is presented in detail in the Appendix. Essentially we break the workforce down into 5 equal groups (quintiles) classified by their wage. Each quintile is taken to have a separate elasticity of labour supply, with low-wage workers having larger values than highly-paid workers. This assumption is motivated by existence of alternative non-market opportunities and welfare payments for the unemployed. Table 1: Alternate Sets of Labour Supply Elasticities
Two alternative assumptions are made concerning three key characteristics of the system. These are the nature of the supply of capital, the elasticities of labour supply (bis), and the proportion of new employment that comes from the unemployed (k). With the supply of capital, we model the two extreme cases outlined in the previous section. These are where the savings function is of a Keynesian character and where the supply of capital is infinitely elastic at the existing post-tax rate of return. For the supply elasticities we use two sets of values. These are identified in Table 1 and labelled as high and low elasticities respectively. Finally we consider two extreme positions, zero and one, with respect to the proportion (k) of the newly employed who come from the registered unemployed. In Tables 2 and 3 we report results from the simulations involving the infinitely elastic supply of capital and the Keynesian savings function respectively. In each table we report the employment change for each quintile of the labour force, the total employment change, the total output change. We also identify the increase in VAT and the fall in the net private sector contribution to the public sector. If the labour subsidy could be incorporated into a tax scheme, this would be the overall change in taxation. In all the simulations reported here there is an increase in total employment and output. Increases in total employment range from 1.45% to 4.00% and 0.76% to 2.84% respectively. In general, the effect on economic activity is greatest for the Keynesian savings function, the higher labour supply elasticities and the higher percentage of workers coming from the unemployment register. For all the simulations there are major increases in employment at the lower end of the labour market. The smallest percentage change in the employment in the poorest quintile is 5.63, with the relatively low labour supply elasticities, the fixed post-tax return to capital and no feedback from reduced unemployment benefit payments. In some simulations there are reductions in employment for the highest quintiles, but these reductions are relatively small. The pattern of employment change is such that output increases by less than employment but in no case does output fail to increase. Although the VAT rate increases by about 5%, where unemployment is assumed to fall as a result of the increased employment the net payment from industry to the public sector falls. If the labour subsidy could be incorporated as part of a tax scheme, in the form of tax rebates, the total tax take would actually fall. However, it should be noted that even where there is no effects from reduced benefit payments, the subsidy still has a positive impact on employment and output. The employment impacts are greater than those identified by Beacon and Monk (1987). There are two main reasons for this. We are adopting a production function where there is a greater elasticity of substitution between inputs. In the Cobb-Douglas case this takes the value of unity, whilst Beacon and Monk used a more conservative value of 0.6. Secondly we treat capital differently and also allow for a more systematic treatment of output effect. We can see by comparing the results in Tables 2 and 3 that the particular treatment of capital supply has an important effect on the employment outcomes and in all cases output rises with the introduction of the subsidy so that there are output as well as substitution effects. www.faxfn.org |
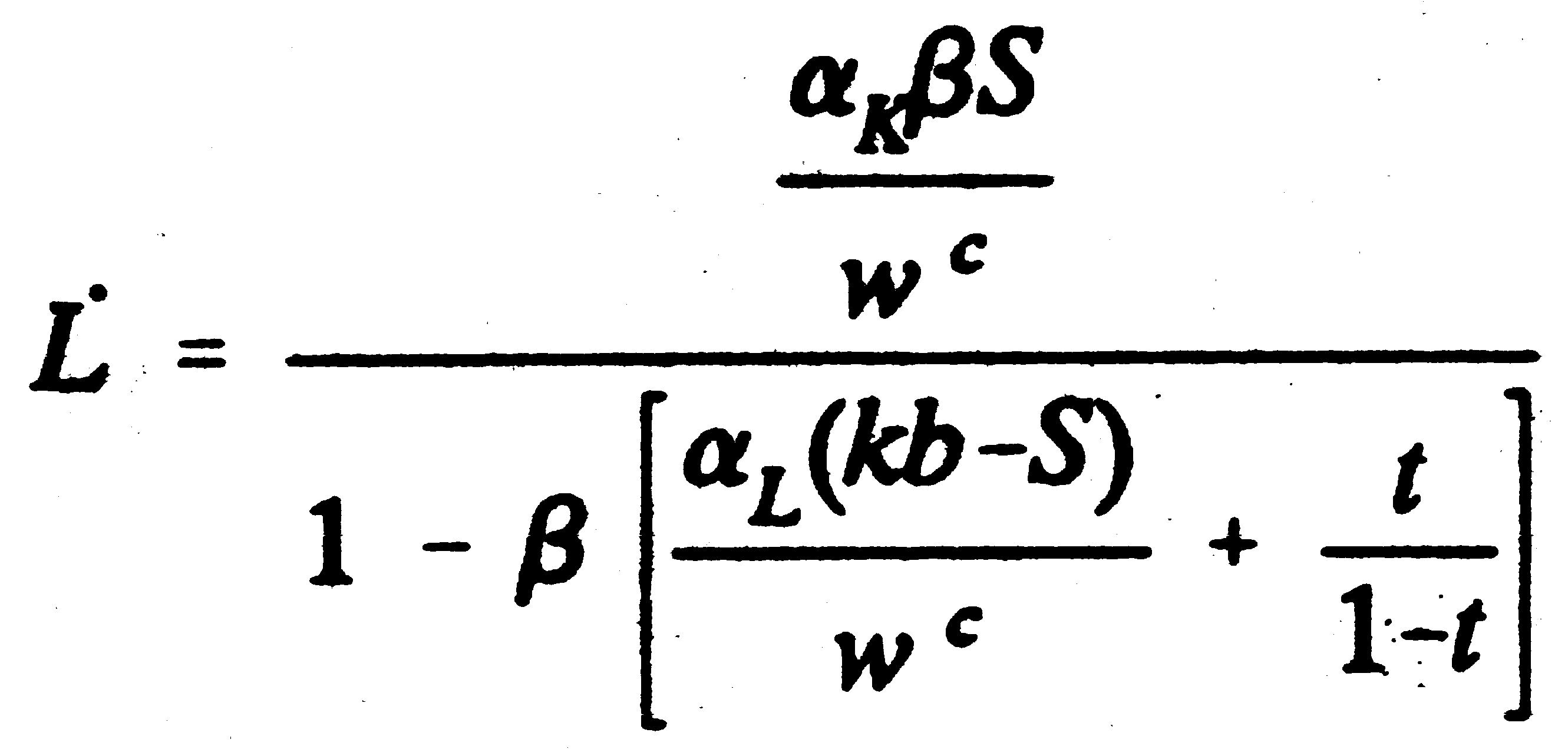 (3.16)
(3.16)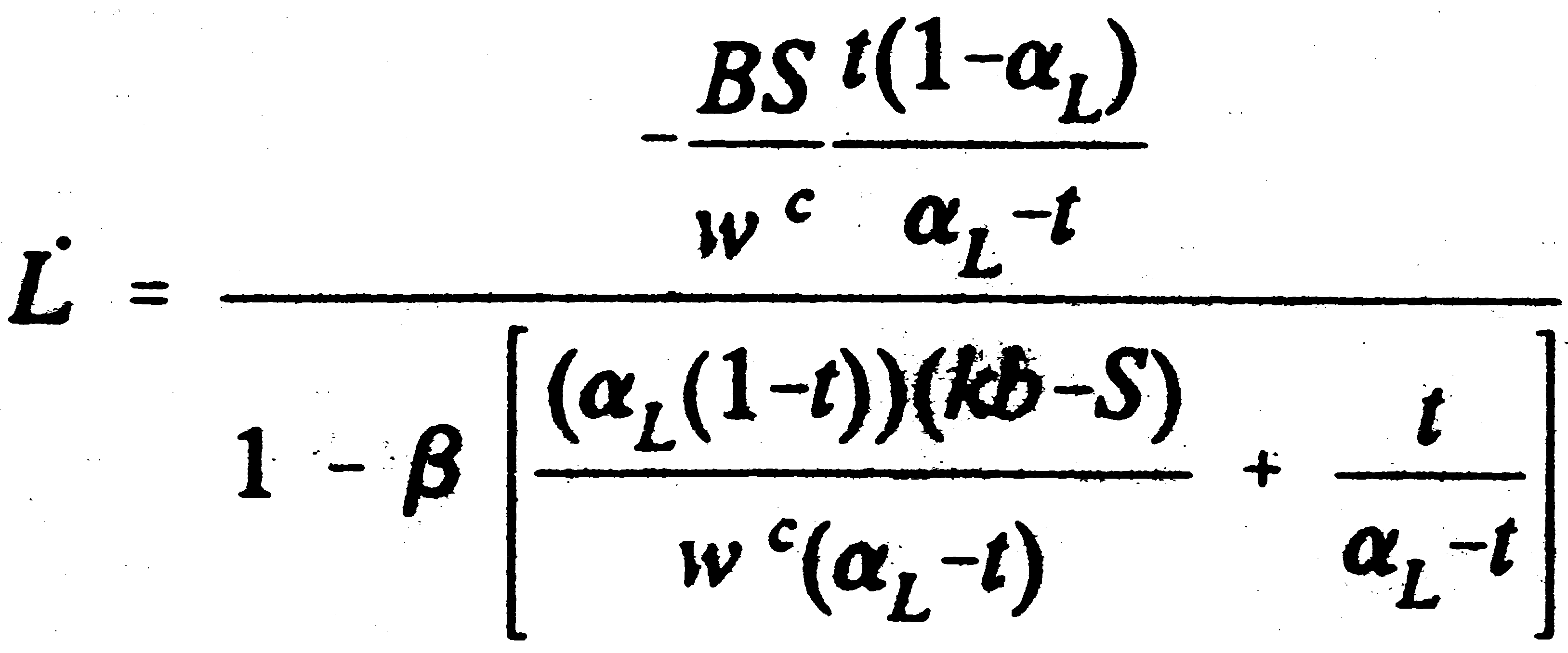 (3.28)
(3.28)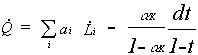 (3.34b)
(3.34b)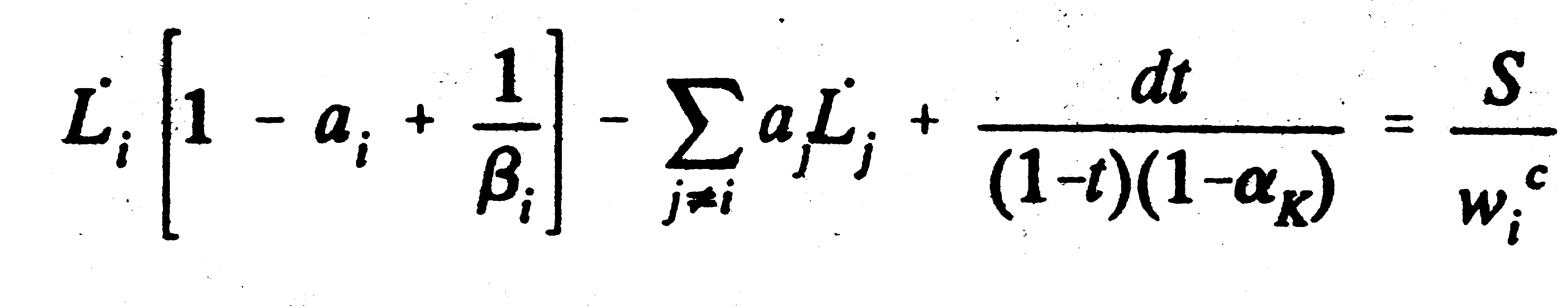 (3.35b)
(3.35b)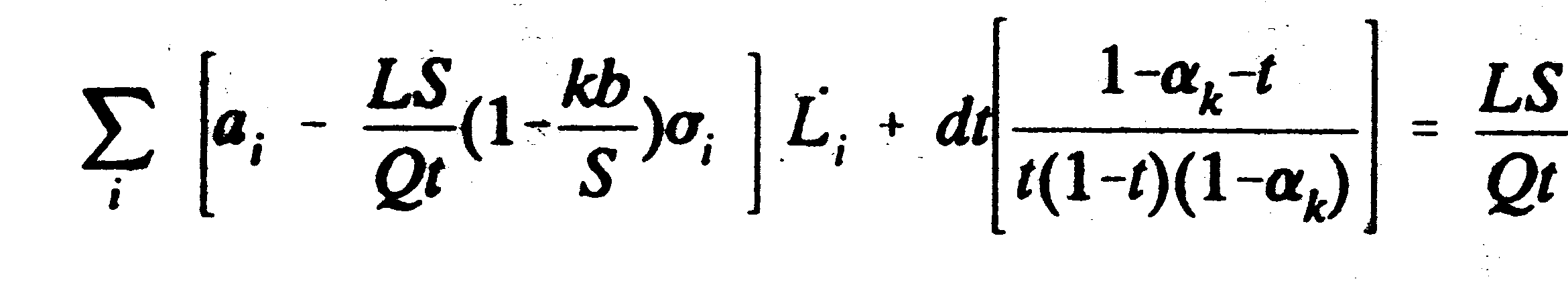 (3.36b)
(3.36b)